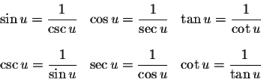PROVING TRIGO IDENTITIES

PROVING TRIGO IDENTITIES

Ok. So we have arrived at the end of the chapter. I know it has been grueling and in many ways torturous (mainly due to the endless list of formulas and exercises we have trying to solve)…. But here we are FINALLY!!! *sign of relieve*

Hence, I have some good news and bad news… i shall start with the bad news, that way we can get it out our heads first. YOU HAVE TO REMEMBER ALL THE FORMULAS FOR THE WHOLE CHAPTER TO DO THIS SECTION…

          

  If u just had a heart attack or have difficulty breathing, I suggest u take a sit IMMEDIATELY and take DEEP BREATHES.., ;) hehehe…

Now for some GOOD NEWS, the formulas you have WORKED SO HARD to cram in your heads can FINALLY be put to some GOOD USE in this part of the chapter. *YAY*

With that aside, I think it is important that I list out a few CRUCIAL identities that may come in handy when trying to prove other trigo identities in this section…

Reciprocal identities

Pythagorean Identities

Quotient Identities

Co-Function Identities

Sum-Difference Formulas 

Double Angle Formulas

Power-Reducing/Half Angle Formulas

Taken from: http://www.sosmath.com/trig/Trig5/trig5/trig5.html

There it is all listed out for u guys… hehehe…. LOOKS a lot I know... But remember:

DON’T STOP BELIEVING!!!

http://www.youtube.com/watch?v=OJz-fOzFbEc

http://www.youtube.com/watch?v=a70-dYvDJZY

EQUIVALENT TRIGONOMETRY EXPRESSION

EQUIVALENT TRIGONOMETRY EXPRESSION

Don’t panic looking at the title. It is a lot simpler then it looks. So let’s begin…J

FIRST OF ALL, let’s look a triangle… J of course after this example u will have to use a unit circle to further your understanding…but here goes

Example :

sinx = a/b 

Given ∠C = π/2 – x

sin ∠C = c/b

cos ∠C = a/b 

tan ∠C = c/a

Therefore,

sinx = cos ∠C , sinx = cos (π/2 – x)

Using the same techniques above… it can be deduced that it is possible to derive a few other similar trigo expressions:

x+(π/2)	π-x
sin x = -cos (X+(π/2))	sin x = sin (π-x)
cos x = sin (X+(π/2))	Cos x = -cos (π-x)
tan x = =cot (X+(π/2))	Tan x = -tan (π-x)
x+π	(π/2)-x
sin x = -cos (x+π)	sin x = cos ((π/2)-x)
cos x = -sin (x+π)	cos x = sin ((π/2)-x)
tan x = cot (x+π)	tan x = cot ((π/2)-x)

Therefore, I know the stuff above is scary looking and all. But honestly the truth is HARD and thus YOU HAVE TO REMEMBER it!! Hehehe… on that note, I hope listing it all out in different colors helps. It helps a ‘lil in my case… but honestly, cramming all that stuff ain’t gonna be easy… hence, I took the liberty to find a parody to do with trigo ( I am sure u all knot the GLEE song “Don’t Stop Believing” J)that just might cheer u up… ALL THE BEST GUYS!!! 

The Move Away From Basics

The MOVE AWAY FROM BASICS

Well, now that the basic of the basics of trigo is covered. Let’s get our hands dirty doing something more ‘interesting’ … ;)

Hence, we will be looking into the TRIGO RATIO & SPECIAL ANGLES…

Ok. Before I start a gentle reminder!! Hehehe… from this section hence forward, there WILL BE A LOT OF MEMORIZATION… that means that theses stuff will not be given as formulas in test and quizzes.. it is up to u to have it IN YOU HEAD!! J

Ok let us begin shall we…

TRIGO RATIOS always come from the SPECIAL TRIANGLE… what are they u ask?? Well look at the triangles below

They are both 90 ̊ (π radian) triangles. Their other sides, however is different. Hence, the other angles are part of the special angles that make up the important special ratios…

Using my ‘knowledge’ of the basic sin,cos and tan in addition to the lengths of the sides of the triangles above..

THIS TABLE IS CRUCIAL… REMEMBER IT!!

Here is a song to remember it by…

http://www.youtube.com/watch?v=07OfkKcxvIA

Another, important note… FORGET NOT THE “CAST RULE”.

The diagram shows which trigo is positive in which quadrant. The “CAST RULE” is important when using related angles with the special angles and finding their ratios. If u still find it kinda confusing, this website may be of great help… J

http://www.worsleyschool.net/science/files/cast/castdiagram.html

CHECK IT OUT>>>

Radian Invasion

I thought my nightmares were alive when Chapter 4 lessons started. Radian (which is not my fav topic) just had to come back to hunt me in colllege.  haizzz... Maybe it will not too bad this time..

Like always... it started off easy. We learnt the basic of the basics like converting (my fav) degrees to (my LEAST fav) radian measures. It was more of a revision but a MUCH NEEDED wan.. :)

Hence, a few examples
Lets just say you want to convert an angle that is in degree to its radian form, a simple formula will be of MAJOR help:

π/180 x (degrees) = radians

In the same way, if you would rather look at your angles in degree form, you will just have to rearrange the formula a 'lil to get:

180/π x (radians) = degrees

Therefore, after this, i think i will not be facing any huge problem converting my radian into degress or vice versa..

OF COURSE, the lesson doesn't stop there.. :)

We were introduced to something relatively new.. well it was new in my case... it was something called ANGULAR VELOCITY

i am sure the word 'VELOCITY' rings a bell.. but you see if velocity is used by itself, it can only be utilised after the distance travelled as been calculated: Which is pretty sad if u want to calculate the velocity for an object that is rotating or moving in a circular motion. But no worries!! There is always a formula to the RESCUE!!! ;)

 it is simply by dividing the angle made(in degree or radian) by the the time(in seconds)

Therefore, to increase understanding and to know more about ANGULAR VELOCITY or maybe just to see how is it use do solve some application questions.... the link below is kinda...COOL!! :) 

http://www.youtube.com/watch?v=mTJaLLi8JVM

And i guess, this comes to the end of the introduction of trigo in radians.. FOR NOW..:)